jueves, 15 de noviembre de 2012
1 Estructura algebraica
En matemáticas, una estructura algebraica es un conjunto de elementos con unas propiedades operacionales determinadas; es decir, lo que define a la estructura del conjunto son las operaciones que se pueden realizar con los elementos de dicho conjunto y las propiedades matemáticas que dichas operaciones poseen. Un objeto matemático constituido por un conjunto no vacío y algunas leyes de composición interna definida en él es una estructura algebraica. Las estructuras algebraicas más importantes son:
| Estructura | Ley interna | Asociatividad | Neutro | Inverso | Conmutatividad |
|---|---|---|---|---|---|
| Magma | |||||
| Semigrupo | |||||
| Monoide | |||||
| Monoide abeliano | |||||
| Grupo | |||||
| Grupo abeliano |
| Estructura (A,+,·) | (A,+) | (A,·) |
|---|---|---|
| Semianillo | Monoide abeliano | Monoide |
| Anillo | Grupo abeliano | Semigrupo |
| Cuerpo | Grupo abeliano | Grupo abeliano |
0 Lenguaje Algebraico
| Lenguaje Algebraico | |
| Un número cualquiera. | m |
| Un número cualquiera aumentado en siete. | m + 7 |
| La diferencia de dos números cualesquiera. | f - q |
| El doble de un número excedido en cinco. | 2x + 5 |
| La división de un número entero entre su antecesor | x/(x-1) |
| La mitad de un número. | d/2 |
| El cuadrado de un número | y^2 |
| La semisuma de dos números | (b+c)/2 |
| Las dos terceras partes de un número disminuidos en cinco es igual a 12. | 2/3 (x-5) = 12 |
| Tres números naturales consecutivos. | x, x + 1, x + 2. |
| La parte mayor de 1200, si la menor es w | 1200 - w |
| El cuadrado de un número aumentado en siete. | b2 + 7 |
| Las tres quintas partes de un número más la mitad de su consecutivo equivalen a tres. | 3/5 p + 1/2 (p+1) = 3 |
| El producto de un número positivo con su antecesor equivalen a 30. | x(x-1) = 30 |
| El cubo de un número más el triple del cuadrado de dicho número. | x3 + 3x2 |
| Signos y Símbolos | |
| + | Además de expresar adición, también es usada para expresar operaciones binarias |
| c ó k | Expresan Términos constantes |
| Primeras letras del abecedario a, b, c,... | Se utilizan para expresar cantidades conocidas |
| Últimas letras del abecedario ...,x, y, z | Se utilizan para expresar incógnitas |
| n | Expresa cualquier número (1,2,3,4,...,n) |
Exponentes y subíndices | Expresar cantidades de la misma especie, de diferente magnitud. |
| Simbología de Conjuntos | |
| {} | conjunto |
| ∈ | Es un elemento del conjunto o pertenece al conjunto. |
| ∉ | No es un elemento del conjunto o no pertenece al conjunto. |
| ⎜ | Tal que. |
| n (C) | Cardinalidad del conjunto C. |
| U | Conjunto Universo. |
| Φ | Conjunto Vacío. |
| ⊆ | Subconjunto de. |
| ⊂ | Subconjunto propio de. |
| ⊄ | No es subconjunto propio de. |
| > | Mayor que. |
| < | Menor que. |
| ≥ | Mayor o igual que. |
| ≤ | Menor o igual que. |
| ∩ | Intersección de conjuntos. |
| ∪ | Unión de Conjuntos. |
| A' | Complemento del conjunto A. |
| = | Simbolo de igualdad. |
| ≠ | No es igual a. |
| ... | El conjunto continúa. |
| ⇔ | Si y sólo si. |
| ∼ | No (es falso que). |
| ∧ | Y |
| ∨ | O |
2 Leyes del álgebra elemental
Propiedades de las operaciones
- La operación de adición (+)
- se escribe

- es conmutativa:
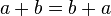
- es asociativa:

- tiene una operación inversa llamada sustracción:
 , que es igual a sumar un número negativo,
, que es igual a sumar un número negativo, 
- tiene un elemento neutro 0 que no altera la suma:

- se escribe
- La operación de multiplicación (×)
- se escribe
 ó
ó 
- es conmutativa:
 =
= 
- es asociativa:

- es abreviada por yuxtaposición:
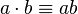
- tiene una operación inversa, para números diferentes a cero, llamada división:
 , que es igual a multiplicar por el recíproco,
, que es igual a multiplicar por el recíproco, 
- tiene un elemento neutro 1 que no altera la multiplicación:

- es distributiva respecto la adición:

- se escribe
- La operación de potenciación
- se escribe

- es una multiplicación repetida:
 (n veces)
(n veces) - no es ni comutativa ni asociativa: en general
 y
y 
- tiene una operación inversa, llamada logaritmo:
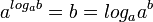
- puede ser escrita en términos de raíz n-ésima:
![\ a^{m/n} \equiv (\sqrt[n]{a^{m}})](http://upload.wikimedia.org/math/9/d/c/9dce189c9cd5c2644b62a96c54e7eb83.png) y por lo tanto las raíces pares de números negativos no existen en el sistema de los números reales. (Ver: sistema de números complejos)
y por lo tanto las raíces pares de números negativos no existen en el sistema de los números reales. (Ver: sistema de números complejos) - es distributiva con respecto a la multiplicación:

- tiene la propiedad:

- tiene la propiedad:
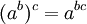
- se escribe
[editar]Orden de las operaciones
Para completar el valor de una expresión, es necesario calcular partes de ella en un orden particular, conocido como el orden de prioridad o precedencia de las operaciones. Primero se calcula los valores de las expresiones encerradas en signos de agrupación (paréntesis, corchetes, llaves), luego las multiplicaciones y divisiones y, por último, sumas y restas.
[editar]Propiedades de la igualdad
La relación de igualdad (=) es:
- reflexiva:

- simétrica: si
 entonces
entonces 
- transitiva: si
 y
y  entonces
entonces 
[editar]Leyes de la igualdad
La relación de igualdad (=) tiene las propiedades siguientes:
- si
 y
y  entonces
entonces  y
y 
- si
 entonces
entonces 
- si dos símbolos son iguales, entonces, uno puede ser sustituido por el otro.
- regularidad de la suma: trabajando con números reales o complejos sucede que si
 entonces
entonces  .
. - regularidad condicional de la multiplicación: si
 y
y  no es cero, entonces
no es cero, entonces  .
.
[editar]Leyes de la desigualdad
La relación de desigualdad (<) tiene las siguientes propiedades:
- de transitividad: si
 y
y  entonces
entonces 
- si
 y
y  entonces
entonces 
- si
 y
y  entonces
entonces 
- si
 y
y 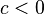 entonces
entonces 
[editar]Regla de los signos
En el producto y en el cociente de números positivos (+) y negativos (-) se cumplen las siguientes reglas:
Suscribirse a:
Comentarios (Atom)
